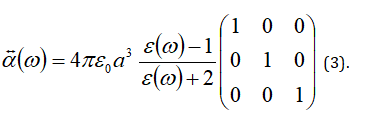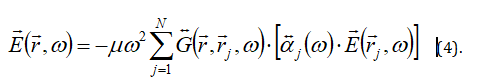¹Centro de Nanociencias y Nanotecnología, Universidad Nacional Autónoma de México, México

²Carretera Tijuana-Ensenada, Ensenada, Baja California CP 22860, México

³Ingeniería Mecatrónica, Universidad Politécnica de Baja California, Mexicali 21376, México

⁴Instituto Tecnológico Superior de Guasave, Carretera Int. entronque a carretera La Brecha SN, Ejido Burrioncito, 81149, Sinaloa México

⁵Instituto Potosino de Investigación Científica y Tecnológica, A.C., SLP México

*Corresponding author: Mufei Xiao, Centro de Nanociencias y Nanotecnología, Universidad Nacional Autónoma de México, km. 107 Carretera Tijuana-Ensenada, Ensenada, Baja California CP 22860, México; Email: [email protected]

Received Date: April 3, 2023

Publication Date: April 24, 2023

Citation: Xiao M, et al. (2023).  Collective Plasmonic Resonances of Metallic Particle Clusters in Zeolite Materials. Catalysis Research. 3(2):12.

Copyright: Xiao M, et al. © (2023). 

ABSTRACT

Based on a microscopic theory for collective resonances of metallic particle clusters, enhanced optical reactions from zeolite materials doped with metallic particles are studied. The influences of particle size, global density, and local tightness are essential for the appearance of collective resonances. Transmission electron microscopy (TEM) was carried out for three zeolite membranes, namely, CuMOR, CuFe₂MOR, and CuFe₃MOR. The TEM images show clearly that metallic particles are squeezed with nanometric distances. Models similar to the experimental TEM images are established as a larger system, where a group of metallic nanoparticles of various sizes is randomly distributed on a surface, which is simulated for the plasmon spectroscopy. Collective resonances were observed, which are related to the tightness, i.e. the average inter-particle distance. The collective resonances stem from the enhanced optical reactions due to the doping of metallic particles into zeolite materials. The study is useful for increasing the catalytic efficiency and yield from zeolite-containing materials.

Keywords: Collective plasmonics; nanoparticles; cluster of metal particles; zeolite catalysts

INTRODUCTION

Zeolites are crystalline microporous aluminosilicates that have found wide-ranging industrial applications in catalysis [1-3], as well as in other processes [4,5]. The main feature that fundamentally distinguishes them from other carriers is a system of voids strictly ordered in shape and size, which are an element of their crystalline structure. Catalysts are materials that allow important reactions to be more selective, faster, and require less energy. Coinage metals (copper, silver, and gold) possess noteworthy optical and electrical properties, are often found as important components in most catalysts, and are known for their high activity as well as many other important properties. Nanoclusters of these metals are widely used in biomedical imaging, remote sensing, labeling, etc. Coinage metal nanostructures possess noteworthy optical, and electrical properties, that are inspiring serious research toward the design and synthesis for potential application in areas such as antibacterial activity, surface-enhanced Raman scattering (SERS)-based detection, and electrochemical sensing. The most recent developments deal with their antiviral applications [6]. Historically, Cu, Ag, and Au have been well-known for their oligodynamic efficacy, antiviral action as well as good biocompatibility, binding receptor inhibition, formation of reactive oxygen species, and phototherapy properties. Thus, a study was conducted to investigate the diagnostic and therapeutic mechanisms of the antivirus ability and mode of action of coinage metals on SARS-CoV-2. This article [6] also draws attention to coinage metal nanomaterial-based approaches to the treatment of other contagious viruses.

It is reported that these metal nanoparticles are novel and effective catalysts; they are also used as a catalyst when deposited on different supports. An effective way to enhance the chemical processes is the introduction of plasmonic nanostructures and particles [7-10]. Particles of metals, such as copper, silver, and gold, are excellent plasmonic media. Surface plasmons and small particle plasmons may be excited by light [11-13]. When metallic particles are crowded within nanometric distances, the local field at the sites of particle locations may be enhanced due to the near-field coupling. Consequently, collective resonances due to the near-field coupling may be excited by external light to form hot spots/points in the materials, and the enhanced local electric field promotes zeolite catalysis as well as other chemical processes.

Heterogeneous catalysis is one of the fundamental processes of chemical technology. Its advantages include the ability to easily separate and reuse the catalyst, easy purification of the product, and the ability to operate in a continuous flow, which opens up potential applications in the fine chemical and pharmaceutical industries [14]. In heterogeneous catalytic reactions, supported metal catalysts in the form of nanoparticles and/or clusters are attracting increasing attention both in industrial production and in environmental remediation [15]. The development of heterogeneous catalysts requires ongoing efforts to understand and develop active centers with improved characteristics for various applications [16].

Metallic nanoparticles, as well as ultra-small sub-nanometer clusters, may have unique and even unexpected physical and chemical properties that make them interesting for potential applications such as catalysis, photocatalysis, electrocatalysis, and optical and chemical sensors, to name but a few. These small particles are easily tunable and provide an economical, atomically efficient use of the supported metal charge [17]. Clusters of a selected size have specific catalytic properties [18].

The stability of nanoparticles can be increased by encapsulating them; in particular, these prospects were discussed in [15]. Important features are given in [19]. Nanoparticle-based catalysis not only plays a key role in the production of fine chemicals such as coupling products, heterocycles, alcohols, carbonyl compounds, acids, etc. but also ensures robust chemical processes. The use of supported metal nanoparticles provides a much better basis than conventional homogeneous and heterogeneous catalysts for tuning reactivity, reusability, and high productivity [20]. The concept of active centers is presented [21]. Varieties of metal species of different sizes (single atoms, nanoclusters, and nanoparticles) exhibit different catalytic behavior [22]. Clusters of a selected size, containing a few atoms, can have noble catalytic properties different from nanoscale or bulk catalysts. Clusters of selected size and composition can also serve as models of catalytic active centers, where the addition or removal of a single atom can have a dramatic effect on their activity and selectivity [23].

In Ref. [17], the optical properties and stability of nano species are discussed. Plasmonic photocatalysis has become a prominent and growing field. It allows the efficient use of sunlight as an abundant and renewable energy source to drive many chemical reactions. For example, plasmonic photocatalysis in materials containing TiO2 and plasmonic nanoparticles (NPs) provides efficient separation of charge carriers and tuning of the optical response to longer wavelengths (visible and near-infrared) [24-26].

In the present work, a microscopic theory for collective plasmonics of metallic particle clusters is introduced, and enhanced optical reactions from zeolite materials doped with metallic particles are studied. Transmission electron microscopy (TEM) was carried out for three zeolite membranes, namely, CuMOR, CuFe₂MOR, and CuFe3MOR. The TEM images show clearly that metallic particles are squeezed with nanometric distances. A larger system, where a group of metallic nanoparticles of various sizes is randomly distributed on a surface, is simulated for plasmon spectroscopy. Collective resonances are observed, which is related to the tightness, i.e. the average inter-particle distance. The paper is organized as follows. In Section 2, the theory is outlined. In Section 3, three TEM images are presented respectively for three zeolite membranes. In Section 4, some numerical calculations based on the theory are presented, and the results are discussed. In Section 5, the work is concluded.

THE THEORY

It is possible to perform a microscopic theoretical analysis based on self-consistent solutions of coupled-dipole clusters of small metallic particles [11-13,27]. The particles are of various sizes and distributed orderly or randomly with a changing density. The local concentrations and shapes may be diversified. The analysis is expected to show a concentration of surface plasmon excitations at the sites of local hot points, and the level of the plasmon excitation is related to the global density of the clusters. The study is primarily aimed to enhance zeolite catalysis, both for Bronsted sites and Lewis sites. It is intended to increase the harvest of zeolites as well as other processes. The results are possibly to be compared and discussed with available experimental results of zeolite catalysis.

Let us now have a close look at the cause of the huge enhancement of the local electrical fields. The extraordinary enhancements cannot be fully explained along with the increased response of the individual metallic particles stemming from either the small-particle and surface-plasmon modes, it is reasonable to conjecture that the interactions between the particles would play an important role and be the principal cause of the huge enhancement. The enhanced responses come mainly from the scattered field from the metallic particles. If the local field driving the particles would be significantly enhanced due to the strong interactions between the particles, the optical response of the whole system would increase strongly.

We introduce a previously established microscopic theory to calculate the optical response as a function of the tightness of the cluster [11-13,27]. The calculation takes two steps, namely solving the self-consistent set of equations that account for all microscopic interactions between the particles, and relating the local field to the scattered field in the observation area. The self-consistent equation for each step can be written as

where   and  are respectively the monochromatic incident field and local field at the frequency  and the  particle site   The field propagator (or dyadic Green’s function) in free space describes the field propagation from   particle to   particle,

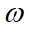
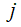
for the vector   and distance   is a unit vector,  is a unit tensor, and   is the wavenumber of light in free space. The polarizability tensor is calculated in the long wavelength electrostatic approximation via the particle’s radius  and its dielectric function  as

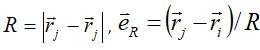
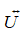
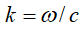
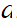
And, after the local field is determined by the proven self-consistent equation, the scattering field at a far field position 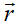 can be calculated as

Therefore, the scattering field can be compared with the incident field and the local field. The enhanced rate is thus determined.

In the equation in Eq. (1), the local field at each particle site is a sum of the contributions from the rest of the particles with various polarizability strengths Eq. (3) and the interactions between particles are included in the field propagators Eq. (2).

Solving the set of equations self-consistently as a standard eigenvalue problem, one expects that the local field can be accurately calculated with the possibility to have resonances. Once the local field is calculated, the observed field at a point far away from the cluster 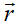  is calculated using the equation in Eq. (4) representing the optical response of the cluster. The details of the field propagators as well as other parameters involved in the numerical simulations can be found in Refs. [11-13,27]. In the calculations, the lengths were normalized to the wavelength.

Transmission Electron Microscopy (TEM)

In this section, let us have a look at some zeolite materials with transmission electron microscopy (TEM). The purpose is to see how the metallic elements are randomly distributed and crowed on a zeolite membrane. Some parameters are essential for the collective resonances to occur, for example, the distances between particles and the size of the particles, etc.

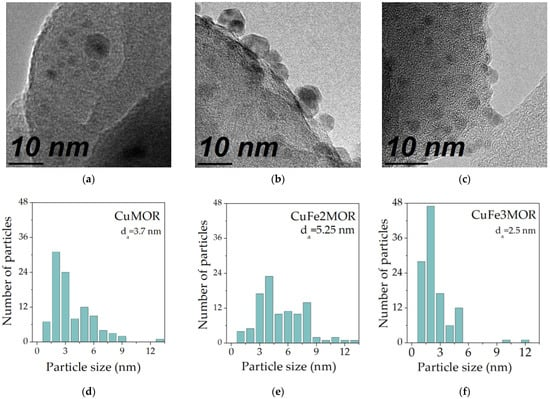
In Figure 1, three TEM images are presented with statistics of the particle size. The experiments were carried out for three zeolite membranes, namely, CuMOR, CuFe₂MOR, and CuFe₃MOR, which all belong to the group of irons coupled mordenite. The size of the particles ranges from 2 nm to 5 nm, and the average inter-particle distance range from 2 to 5 nm too.

The TEM images in Figure 1 show that in zeolite materials, metallic elements can be crowed at a nanometer distance, which fulfills the conditions for plasmons of individual particles to interact via near-field coupling, so that the collective plasmon show enhanced hot spots, namely, local collective resonances. In a global account, clusters of metallic particles will bring up global collective resonances. Both the local, i.e. the hot spots and the global collective resonances are to be presented in the next Section. The numerical simulations would offer guidance for experimental plasmon spectroscopy.

Figure 1: Transmission electron microscopy (TEM) images for three zeolite membranes, as well as the statistics of particle size. (a) and (d) are for CuMOR, (b) and (c) are for CuFe₂MOR, and (c) and (f) are for CuFe₃MOR.

NUMERICAL RESULTS

There are two ways to collect the scattered light, in the near field and far field. Near field microscopy (see for instance Ref. [12] and the references therein) makes use of the local probe to collect the near field near the sample surface. The advantage of near field miscopy is the breakthrough of resolution limit, i.e. one sees the hot points where light is scattered near the particles. Another way to collect scattering fields is in the far field. Optical probes are fixed at certain distances, somewhere from the sample surface, and the far field is collected. The far-field collection is true of traditional optical detection, and it is easier to be implemented.

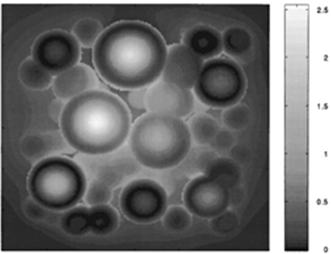
For numerical calculations, both methods, namely near and far collections, have been simulated, and some representative results can be found in Refs. [11-13,28]. In Figure 2, a picture is reproduced from data for Ref. [12], which shows a near-field microscopic image of a group of nanometric silver particles with various sizes, randomly distributed on a surface.

In Figure 2, near-field optical microscopy is simulated with a probe tightly scanning above a surface 600nm X 600nm where about 50 silver spherical particles of various sizes are randomly distributed. One can see from Figure 2 that since the near-field information is collected, the microscopy resolves most of the particles. Conventional optical microscopy is fundamentally limited in resolution within half of the wavelength λ/2. Near-field microscopy resolves details and shows that light is enhanced somewhere. One may referrer the area where light is enhanced as hot points.

 

(a)

(b)

Figure 2: (a) About 50 silver spherical particles of various sizes are randomly distributed on a surface of 600 nm X 600 nm. (b) Optical microscopy with a probe scanning 1 nm above the particles. The brightness refers to the incident light.

The resolution of the microscopy weakens when the probe is leaving the sample surface. In this case, the far field will dominate the collected signals, and details are barely shown. On the other hand, the hot pints can still be seen in some places. More results from optical microscopy with various degrees of near-field participation can be found in Refs. [11-13,28].

It is worth mentioning that the theory is not limited to randomly distributed particle clusters. It is possible also for dealing with ordered distributions. For some applications, the simulations provide valuable accounts. In Ref. [11], a group of particles is orderly distributed, and clearly, the scattered field is engineered to a direction, which demonstrated that it is possible to make use of ordered particles in structures to purposely guide light.

Let us now have a look at a global range. An optical probe is supposed to be away from the sample at a fixed position. This a convenient method for optical detection, widely used in optical spectroscopies. All microscopic images are mixed into a single channel. Therefore, the simulation provides information for the collective plasmonics of particle clusters including resonances. An image from the simulation is presented in Figure 3.

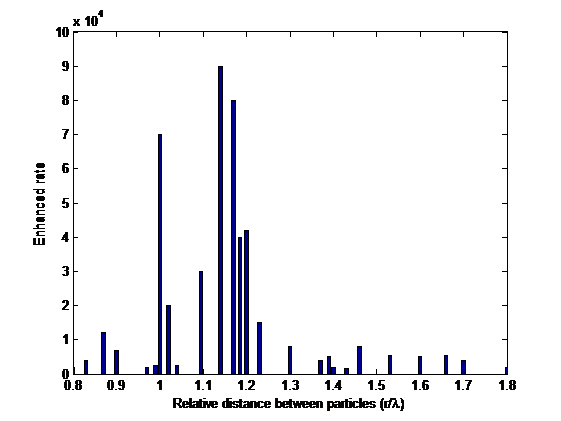
The normalized lengths marked in Figure 3 for a wavelength of 633 nm correspond to a range of about 500 nm to 800 nm, respectively. In Figure 3, the resonances are a notable feature. When the particles are far away from each other, the responses are small. When the tightness increases there are possibilities to excite the resonances and the scattered field is enhanced strongly by several orders of magnitude. If the particles are further pushed together, the field strength decreases again. Note that the tightness is different from the density. It takes into account the distances between particles.

The relative distance is the average inter-particle distance of a cluster of 50 silver particles. Therefore, the relative distance represents a measure of the tightness of the particles. In Figure 3, it is shown that resonance is excited near the wavelength distance. A stronger resonance appears at about 1.2λ , and a weaker resonance appears at about  0.8λ . When the distance is enlarged, there is no resonance at all. One realizes that an enhancement as strong as 9 × 10¹⁴ is possible for clusters of relative distance comparable to the wavelength of the incident light.

Figure 3: Optical response enhanced rate as a function of the relative distance between 50 particles.

The above behavior of the optical response appears consistent with experimental results reported in [7-10,27], i.e. the optical response increases with the density of the silver clusters, and the enhancement reaches a peak before becoming saturated. The above model simulations are suitable for samples of zeolites, such as the three zeolite membranes shown in Section 2. In the succeeding section, images from our experiments are to be presented. CuMOR, CuFe₂MOR, and CuFe3MOR have been extensively studied for catalysis applications. The existence of a large number of metallic nanoparticles in the zeolite materials helps to enhance the optical responses, and strong light interaction increases in general the catalytic efficiency and yield from zeolite-containing materials.

CONCLUSIONS

In conclusion, an optical response can be resonantly and dramatically enhanced by doping metallic particles, and the density or tightness of the particle clusters is essential for exciting the collective resonances. When the relative distance is about the wavelength of the incident light, the resonances appear. This enhancement would be helpful for zeolite catalysis as well as for other chemistry and material processes. Transmission electron microscopy (TEM) was carried out for three zeolite membranes, namely, CuMOR, CuFe₂MOR, and CuFe₃MOR. The TEM images show clearly that metallic particles are squeezed with nanometric distances. Models similar to the experimental TEM images are used to simulate a larger system, where a group of metallic nanoparticles of various sizes is randomly distributed on a surface, which is simulated for plasmon spectroscopy. Collective resonances were observed, which is related to the tightness, i.e. the average inter-particle distance. The collective resonances stem from the enhanced optical reactions due to the doping of metallic particles into zeolite materials. The study is useful for increasing the catalytic efficiency and yield from zeolite-containing materials.

ACKNOWLEDGMENTS

This research was funded by DGAPA‐PAPIIT Grant IG101623 and CONACYT, “Basic Science Project A1‐S‐33492”.

REFERENCES

1. Hua Z Yang Y, Liu J. (2023). Direct hydrogenation of carbon dioxide to value-added aromatics. Coord. Chem Rev. 478:214982.
2. Sanchez-Lopez P, Kotolevich Y, Yocupicio-Gaxiola RJ, Antunez-Garcia J, Chowdari RK, Petranovskii V, et al. (2021). Recent Advances in Catalysis Based on Transition Metals Supported on Zeolites. Front Chem. 9:716745.
3. Gellé A, Jin T, De La Garza L, Price Gareth G, Besteiro D, Moores L. (2020). Applications of plasmon-enhanced nanocatalysis to organic transformations. Chem Rev. 120:986-1041.
4. Samanta NS, Das PP, Mondal P, Changmai M, Purkait MK. (2022). Critical review on the synthesis and advancement of industrial and biomass waste-based zeolites and their applications in gas adsorption and biomedical studies. J Indian Chem Soc. 99:100761.
5. Chin C, Kamin Z, Bahrun MHV, Bono A. (2023). The Production of Industrial-Grade Oxygen from Air by Pressure Swing Adsorption. Int J Chem Eng. 2023:2308227.
6. Mushtaq A, Iqbal M.Z, Kong X. (2022). Antiviral effects of coinage metal-based nanomaterials to combat COVID-19 and its variants. J Mat Chem. B. 10:5323-5343.
7. Zhang X, Ke X, Du A, Zhu A. (2014). Plasmonic nanostructures to enhance catalytic performance of zeolites under visible light. Sci Rep. 4:3805.
8. Linic S, Christopher P, Ingram DB. (2011). Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat Mater. 10: 911–921.
9. Maier SA, Kik PG, Atwater HA, Meltzer S, Harel E, Koel BE, et al. (2003). Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat Mater. 2:229–232.
10. Wang F, Li C, Chen H, Jiang R, Sun LD, Li Q, et al. (2013). Plasmonic harvesting of light energy for Suzuki coupling reactions. J Am Chem Soc. 135:5588–5601.
11. Xiao M, Bozhevolnyi S. (2001). Resonant field enhancement by a finite-size periodic array of surface scatterers. J Phys Condens Matter. 13:3001.
12. Xiao M. (1997). Theoretical treatment for scattering scanning near-field optical microscopy. J Opt Soc Am A. 14:2977-2984.
13. Xiao M, Zayats A, Siqueiros J. (1997) Scattering of surface-plasmon polaritons by dipoles near a surface: Optical near-field localization. Phys Rev B. 55:1824.
14. Dai H, Yang Q. (2022). The importance of interdiscipline in heterogeneous asymmetric catalysis. Chem Catalysis. 2:2840-2851.
15. Li M, Yang Y, Yu D, Li W, Ning X, Wan R, Zhu H, Mao J. (2023) Recent advances on the construction of encapsulated catalyst for catalytic applications. Nano Res. 16:3451-3474.
16. Chavez S, Werghi B, Sanroman Gutierrez KM, Chen R, Lall S, Cargnello M. (2023). Studying, Promoting, Exploiting, and Predicting Catalyst Dynamics: the Next Frontier in Heterogeneous Catalysis. J Phys Chem C. 127:2127-2146.
17. Jašík J, Fortunelli A, Vajda I. (2022). Exploring the materials space in the smallest particle size range: from heterogeneous catalysis to electrocatalysis and photocatalysis. Phys Chem Chem Phys. 24:12083-12115.
18. Kashyap RK, Parammal MJ, Pillai PP. (2022). Effect of Nanoparticle Size on Plasmonic Heat-Driven Organic Transformation. Chem Nano Mat. 8:e202200252.
19. Jing W, Shen H, Qin R, Wu Q, Liu K, Zheng N. (2022). Surface and Interface Coordination Chemistry Learned from Model Heterogeneous Metal Nanocatalysts: From Atomically Dispersed Catalysts to Atomically Precise Clusters. Chem Rev in Press.
20. Baroliya PK, Chopra J, Pal T, Maiti S. (2021). Al-Thabaiti, S.A., Mokhtar, M., Maiti, D. Supported Metal Nanoparticles Assisted Catalysis: A Broad Concept in Functionalization of Ubiquitous C−H Bonds. Chem Cat Chem 13:4655-4678.
21. Vogt C, Weckhuysen BM. (2022). The concept of the active site in heterogeneous catalysis. Nat Rev Chem. 6:89-111.
22. Liu L, Corma A. (2018). Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles. Chem Rev. 118:4981-5079.
23. Halder A, Curtiss LA, Fortunelli A, Vajda S. (2018). Perspective: Size selected clusters for catalysis and electrochemistry. J Chem Phys. 148:110901.
24. Li J, Zhang Y, Huang Y, Bing L, Li B, Jing L, et al. (2022). Noble-metal free plasmonic nanomaterials for enhanced photocatalytic applications-A review. Nano Res. 15:10268–10291.
25. Mo F, Zhou Q, He Y. (2022). Nano–Ag: Environmental applications and perspectives. Sci Total Environ. 829:154644.
26. Zhao J, Wang J, Brock, AJ, Zhu H. (2022). Plasmonic heterogeneous catalysis for organic transformations. J Photochem Photobiol C. 52:100539.
27. Wei J, Liu J, Xiao M. (2011). Giant optical nonlinearity of silver-doped silicon thin film at low power input: laser-triggered cluster resonance. App Phys A. 104:1031-1037.
28. Bozhevolnyi S, Xiao M, Hvam J. (1999). Polarization resolved imaging with reflection near-field optical microscope. J Opt Soc Am A. 16:2649-2657.