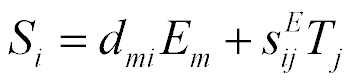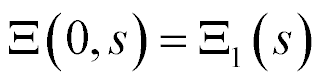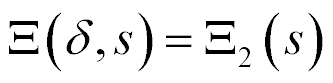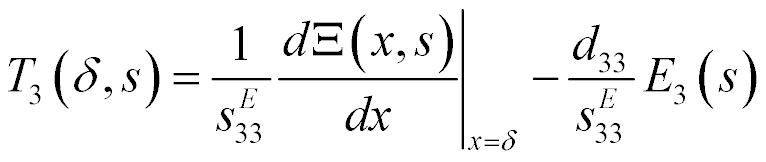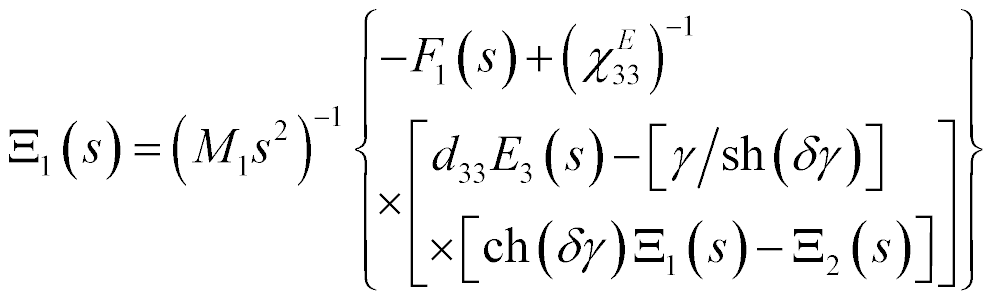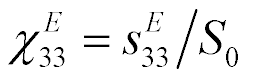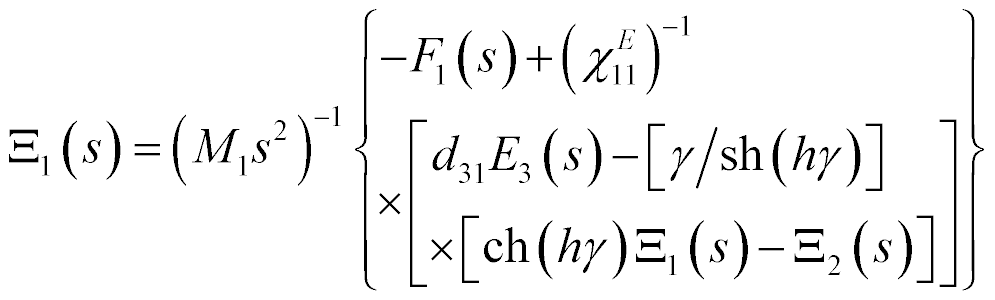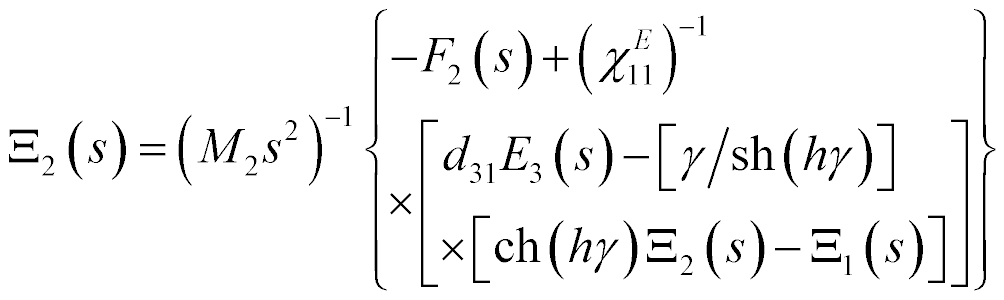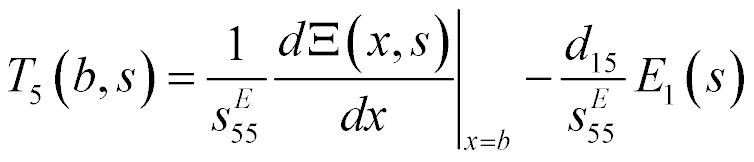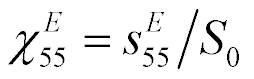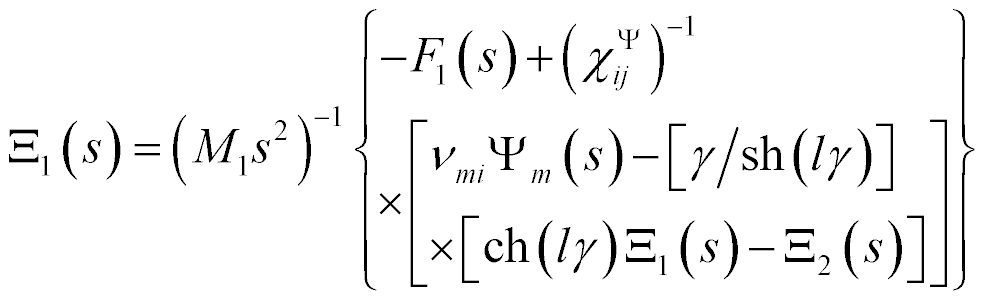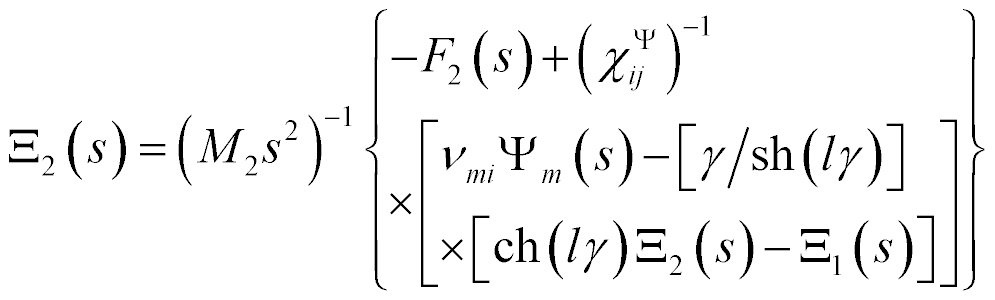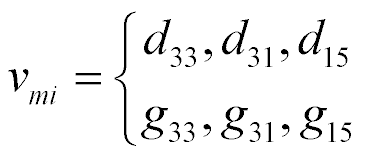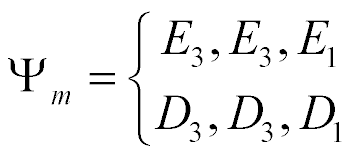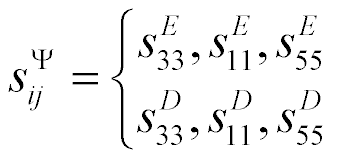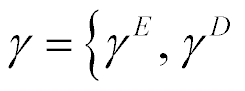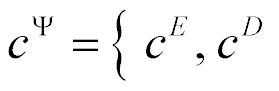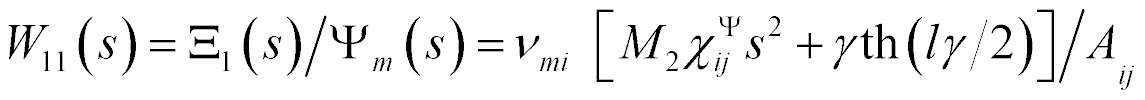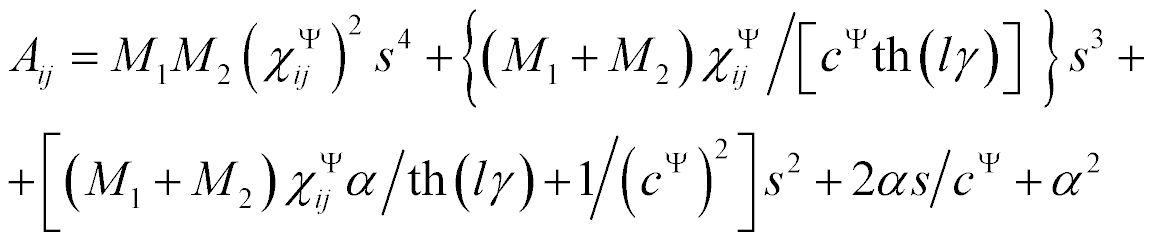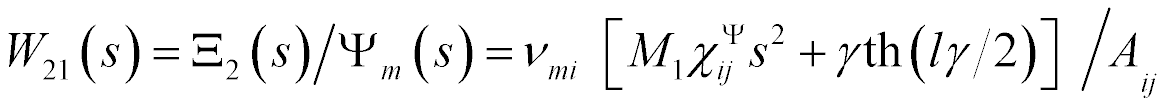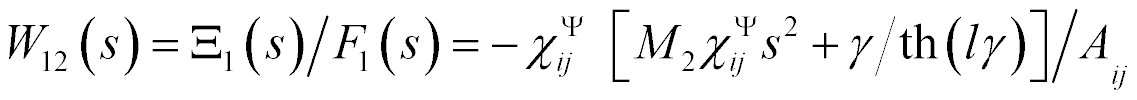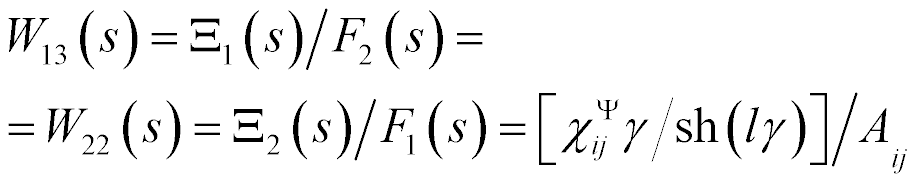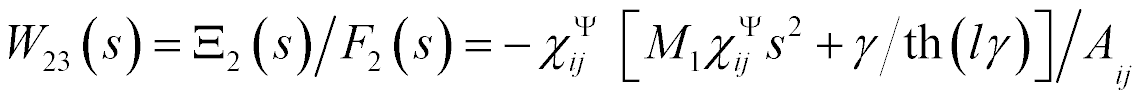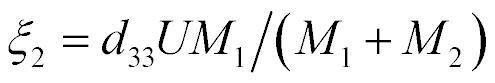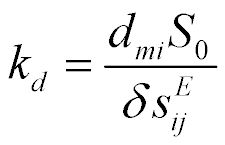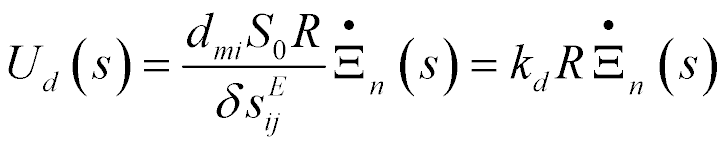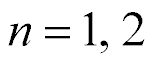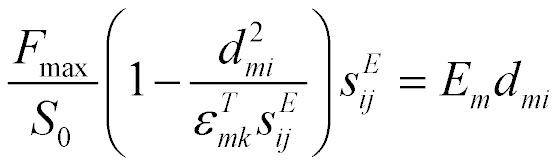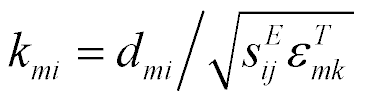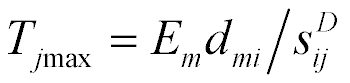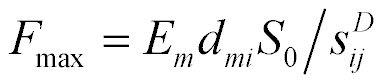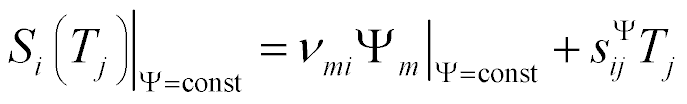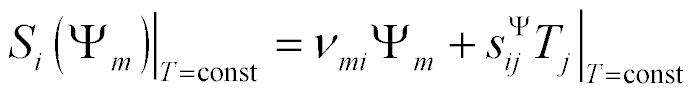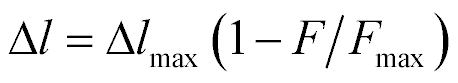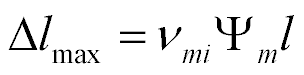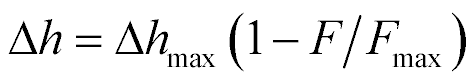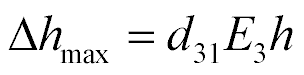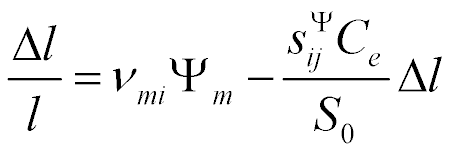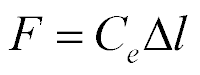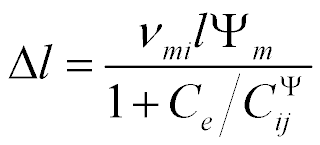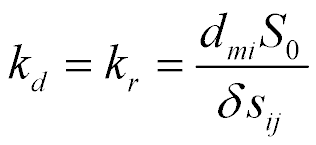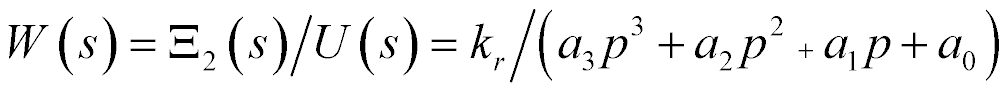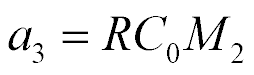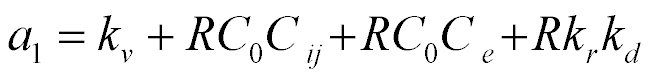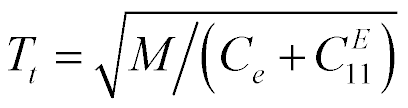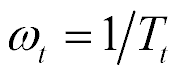National Research University of Electronic Technology, MIET, Moscow, Russia

*Corresponding Author: Afonin SM, National Research University of Electronic Technology, MIET, Moscow, Russia, Tel: 4997102233, Email: [email protected]

Received Date: October 17, 2022

Published Date: December 05, 2022

Citation: Afonin SM. (2022). A Piezo Drive for Nano Chemistry Research. Catalysis Research. 2(1):03.

Copyright: Afonin SM © 2022

ABSTRACT

The mathematical model of a piezo drive is determined for nano chemistry research. The structural schemes of a piezo drive are obtained for nano chemistry research. The matrix equation is constructed for a piezo drive.

Keywords: Piezo drive, Structural scheme, Nano chemistry research

INTRODUCTION

The piezo drive works on basis of the reverse piezoelectric effect [8-52]

where , ,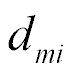 , , 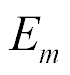, 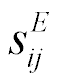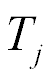are the relative deformation, piezo module, strength electric field, elastic compliance, strength mechanical field, i, j, m are the indexes.

The differential equation is written [8-52]

here, 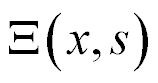, s, x, y are the transform of the deformation, the parameter Laplace transform, the coordinate, the propagation factor. For the longitudinal piezo drive we have at  x = 0 the deformation

  and at     .

Its decision is written

The system for the longitudinal piezo drive is obtained [14 − 26] for 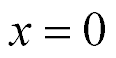  and 

The mathematical model is written

where  ,  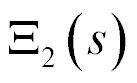 are the transforms of the deformations,  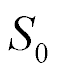 is cross sectional area.

The system for the transverse piezo drive is determined for 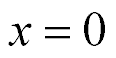  and 

The mathematical model of this drive has the form

The system for the shift piezo drive is written for  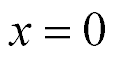 and 

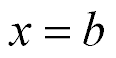
The mathematical model is written

At   and   for 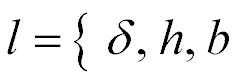  the system in general is obtained

Therefore, the mathematical model in general of a piezo drive is determined on Figure 1

where,

 

Figure 1: In general, structural scheme of piezo drive.

The mathematical model of drive on Figure 1 is used for nano chemistry research. The matrix of deformations is written

where the functions are

The settled longitudinal deformations are determined

For 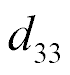  = 4×10^-10 m/V, 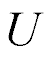= 25 V,   = 1 kg, 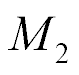  = 4 kg we have the settled deformations   = 8 nm,   = 2 nm and 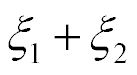  = 10 nm at error 10%.

To calculate the back electromotive force of the piezo drive, we use the equation of the direct piezoelectric effect [8-16]

where 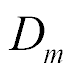 ,   are the electric induction and the permittivity, i, m, k are the indexes, The direct coefficient 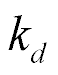  for the piezo drive is written

The transform of the voltage for the back electromotive force of the piezo drive on Figure 2 has the form

 ,   

where 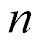  is the number of the face.

Figure 2: Structural scheme of piezo drive with back electromotive force.

Consider the influence of the back electromotive force of the piezo drive on its static deformation.

At voltage control the maximum mechanical stress and the maximum force are written

At current control the maximum force has the form

where 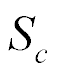 ,  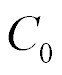 are the sectional area of the capacitor and the capacitor capacitance.

Therefore,

and

where   is the electromechanical coupling coefficient.

For current control of the piezo drive we get the expressions

The elastic compliance   takes the form  ,

where  . Therefore, 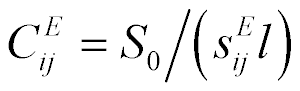  is the stiffness of drive at voltage control,  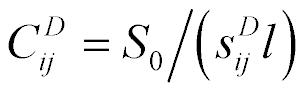 is the stiffness of drive at current control,  ,  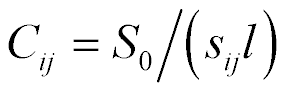 is the stiffness of drive. The stiffness of a piezo drive at open electrodes increases then the stiffness at closed electrodes.

From the equation of electroelasticity the mechanical characteristic 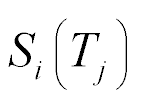  [11-26] is determined

and the adjustment characteristic 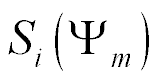  [11-26] is obtained

The mechanical characteristic is written

where 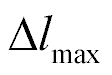  is the maximum of the deformation and  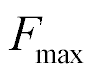 is the maximum of the force. The mechanical characteristic of the transverse piezo drive is determined

At 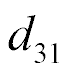  = 2∙10^-10 m/V,  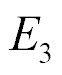 = 0.5∙10⁵ V/m,   = 2.5∙10^-2 m, 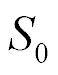  = 1.5∙10^-5 m²,   = 15∙10^-12 m²/N the parameters are found   = 250 nm and 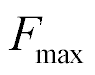  = 10 N at error 10%

The deformation of a piezo drive at elastic load has the form

The adjustment characteristic of a piezo drive is written

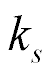We get in general the elastic compliance  and the coefficient   of the change of elastic compliance

The direct and reverse coefficients of a piezo drive in the form

From Figure 2 we get the structural scheme Figure 3 of a piezo drive at one fixed face and elastic-inertial load.

Figure 3: Structural scheme of drive.

The expression on voltage for Figure 3 has form

 , 

 , 

here 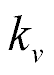  is the damping coefficient.

For the transverse piezo drive at 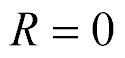  the expression on voltage is obtained

 ,   

For 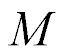  = 1 kg,   = 0.1×10⁷ N/m, 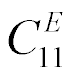  = 1.5×10⁷ N/m we have  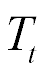 = 0.25×10^-3 s,  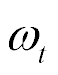 = 4×10³ s^-1 at error 10%.

The settled transverse deformation has the form

For 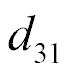  = 2∙10^-10 m/V,  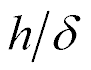 = 25,   = 0.1 the coefficient is determined 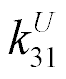  = 4.5 nm/V at error 10%

CONCLUSION

The mathematical model and the structural schemes of a piezo drive are obtained for nano chemistry research. The matrix of the deformations of a piezo drive is constructed. The parameters of a piezo drive are determined.

REFERENCES

1. Schultz J, Ueda J, Asada H (2017) Cellular Actuators. Butterworth-Heinemann Publisher, Oxford, 382 p.
2. Afonin SM. (2006) Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics. 74(3): 943-948. doi:10.1134/S1064562406060391.
3. Uchino K. (1997). Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. p: 350.
4. Afonin SM. (2005). Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 50(2): 77-82. doi:10.1134/1.1881716.
5. Afonin SM. (2008). Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics 53(3): 137-143. doi:10.1134/S1028335808030063.
6. Afonin SM. (2006). Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics 73(2): 307-313. doi:10.1134/S1064562406020402.
7. Cady WG. (1946). Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London. p: 806.
8. Mason W, editor (1964). Physical Acoustics: Principles and Methods. Vol. 1. Part A. Methods and Devices. Academic Press, New York. p: 515.
9. Yang Y, Tang L. (2009). Equivalent circuit modeling of piezoelectric energy harvesters. Journal of Intelligent Material Systems and Structures. 20(18): 2223-2235. doi:10.1177/1045389X09351757.
10. Zwillinger D. (1989). Handbook of Differential Equations. Academic Press, Boston. p: 673.
11. Afonin SM. (2006). A generalized structural-parametric model of an elecromagnetoelastic converter for nano- and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano- and micrometric movement control systems. Journal of Computer and Systems Sciences International. 45(2): 317-325. doi:10.1134/S106423070602016X.
12. Afonin SM. (2006). Generalized structural-parametric model of an electromagnetoelastic converter for control systems of nano-and micrometric movements: IV. Investigation and calculation of characteristics of step-piezodrive of nano-and micrometric movements. Journal of Computer and Systems Sciences International. 45(6: 1006-1013. doi:10.1134/S1064230706060153.
13. Afonin SM. (2016). Decision wave equation and block diagram of electromagnetoelastic actuator nano- and microdisplacement for communications systems. International Journal of Information and Communication Sciences. 1(2): 22-29. doi:10.11648/j.ijics.20160102.12.
14. Afonin SM. (2015). Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York. p: 225-242.
15. Afonin SM. (2017). A structuralparametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J. Nova Science, New York. 19: 259-284.
16. Afonin SM. (2018). Electromagnetoelastic nano- and microactuators for mechatronic systems. Russian Engineering Research 38(12): 938-944. doi:10.3103/S1068798X18120328.
17. Afonin SM. (2012). Nano- and micro-scale piezomotors. Russian Engineering Research. 32(7-8): 519-522, doi:10.3103/S1068798X12060032.
18. Afonin SM. (2007). Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers, Mechanics of Solids. 42(1): 43-49. doi:10.3103/S0025654407010062.
19. Afonin SM. (2014). Stability of strain control systems of nano-and microdisplacement piezotransducers. Mechanics of Solids 49(2): 196-207. doi:10.3103/S0025654414020095.
20. Afonin SM. (2017). Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics 5(1): 9-15.  doi:10.12691/ijp-5-1-2.
21. Afonin SM. (2019). Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 7(2): 50-57. doi:10.12691/ijp-7-2-3.
22. Afonin SM. (2021). Calculation deformation of an engine for nano biomedical research. International Journal of Biomed Research 1(5): 1-4. doi:10.31579/IJBR-2021/028.
23. Afonin SM. (2021). Precision engine for nanobiomedical research. Biomedical Research and Clinical Reviews. 3(4): 1-5. doi:10.31579/2692-9406/051.
24. Afonin SM. (2016). Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 3(4): 31-38.
25. Afonin SM. (2018). Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators 7(1): 1-9. doi: 10.3390/act7010006.
26. Afonin SM. (2019). Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators 8(3): 52. doi: 10.3390/act8030052.
27. Afonin SM. (2016). Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59. doi: 10.11648/j.ijtam.20160202.15.
28. Afonin SM. (2010). Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids. 45(1): 123-132, doi:10.3103/S0025654410010152.
29. Afonin SM. (2018). Electromagnetoelastic Actuator for Nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 18(2): 19-23.  doi:10.17406/GJRE.
30. Afonin SM. (2018). Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology, Proceedings of the 2018 IEEE Conference EIConRus. p:1698-1701. doi:10.1109/EIConRus.2018.8317432.
31. Afonin SM. (2018). A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Transactions on Networks and Communications 6(3): 1-9. doi:10.14738/tnc.63.4641.
32. Afonin SM. (2019). Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems, Transactions on Networks and Communications. 7(3): 11-21. doi:10.14738/tnc.73.6564.
33. Afonin SM. (2020). Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transactions on Networks and Communications. 8(1): 8-15. doi:10.14738/tnc.81.7775.
34. Afonin SM. (2020). A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology, Transactions on Machine Learning and Artificial Intelligence. 8(4): 23-33. doi:10.14738/tmlai.84.8476.
35. Afonin SM. (2020). Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Applied System Innovation. 3(4): 1-7. doi:10.3390/asi3040053.
36. Afonin SM. (2021). Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Applied System Innovation 4(3): 1-11. doi:10.3390/asi4030047.
37. Afonin SM. (2020). Structural scheme actuator for nano research. COJ Reviews and Research. 2(5): 1-3. doi:10.31031/COJRR.2020.02.000548.
38. Afonin SM. (2018). Structural–parametric model electroelastic actuator nano- and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences. 3(5): 306-309. doi:10.15406/mojes.2018.03.00104.
39. Afonin SM. (2018). Electromagnetoelastic actuator for large telescopes. Aeronautics and Aerospace Open Access Journal. 2(5): 270-272. doi:10.15406/aaoaj.2018.02.00060.
40. Afonin SM. (2019). Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery & Case Studies Open Access Journal. 3(3): 307–309. doi:10.32474/SCSOAJ.2019.03.000165.
41. Afonin SM. (2019). Piezo actuators for nanomedicine research. MOJ Applied Bionics and Biomechanics 3(2): 56-57. doi:10.15406/mojabb.2019.03.00099.
42. Afonin SM. (2019). Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ Applied Bionics and Biomechanics. 3(6): 137-140. doi:10.15406/mojabb.2019.03.00121.
43. Afonin SM. (2020). Multilayer piezo engine for nanomedicine research. MOJ Applied Bionics and Biomechanics. 4(2): 30-31. doi:10.15406/mojabb.2020.04.00128.
44. Afonin SM. (2021). Structural scheme of electromagnetoelastic actuator for nano biomechanics. MOJ Applied Bionics and Biomechanics.  5(2): 36-39. doi:10.15406/mojabb.2021.05.00154.
45. Afonin SM. (2020). Multilayer engine for microsurgery and nano biomedicine. Surgery & Case Studies Open Access Journal. 4(4): 423-425. doi:10.32474/SCSOAJ.2020.04.000193.
46. Afonin SM. (2019). A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York 22: 169-186.
47. Afonin SM. (2020). Electroelastic digital-to-analog converter actuator nano and microdisplacement for nanotechnology. Chapter 6 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 24: 205-218.
48. Afonin SM. (2021). Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York, 25: 251-266. doi:10.52305/TANO4731.
49. Afonin SM. (2022). An absolute stability of nanomechatronics system with electroelastic actuator. Chapter 9 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 27: 183-198. doi:10.52305/YOPZ1532.
50. Afonin SM. (2021). Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russian Engineering Research. 41(4): 285-288. doi:10.3103/S1068798X21040031.
51. Nalwa HS, editor (2004) Encyclopedia of Nanoscience and Nanotechnology. Los Angeles: American Scientific Publishers. 10: 11-25.
52. Bhushan B, editor (2004) Springer Handbook of Nanotechnology. New York: Springer. 1222.