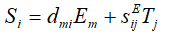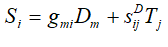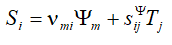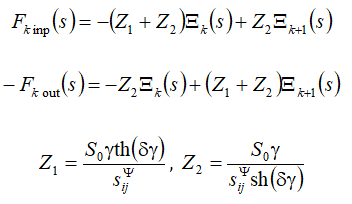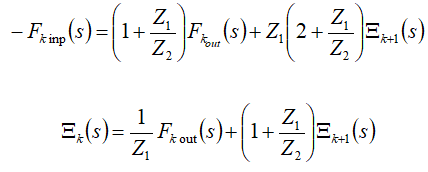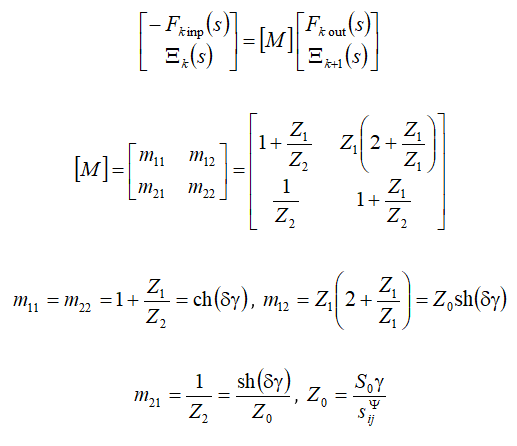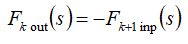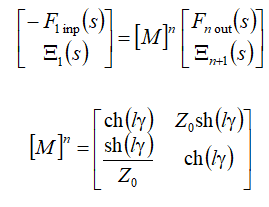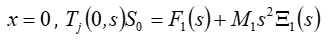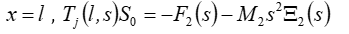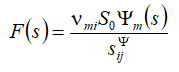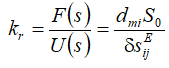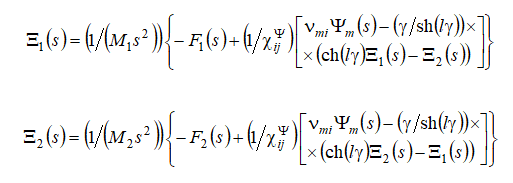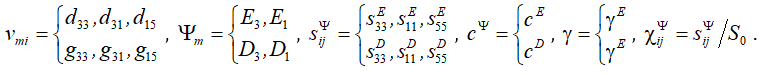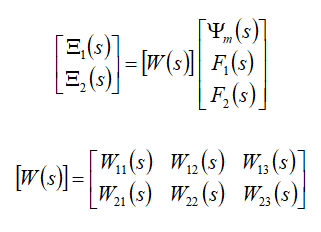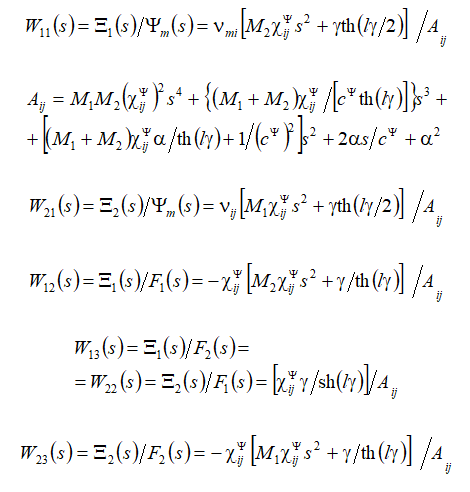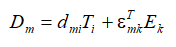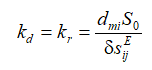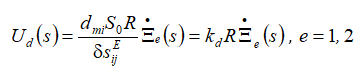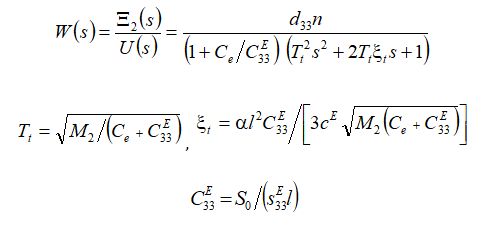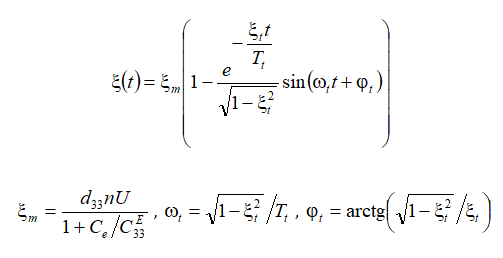National Research University of Electronic Technology, MIET, Moscow, Russia

*Corresponding author: Afonin Sergey Mikhailovich, National Research University of Electronic Technology, MIET, 124498, Moscow, Russia, E-mail: [email protected]

Received Date: July 18, 2024

Publication Date: October 21, 2024

Citation: Afonin SM. (2024). A Compound Piezo Drive for Nanotechnology and Nanochemistry Research. Catalysis Research. 4(1):18.

Copyright: Afonin SM. © (2024).

ABSTRACT

For nanotechnology and nanochemistry research a compound piezo drive is applied in nanomechatronics systems. A compound piezo drive for nanotechnology and nanochemistry is used in scanning microscopy, adaptive optics amd interferometry. The model and scheme of a compound piezo drive is determined. Its functions and matrix deformations are founded. The schemes and parameters of the compound piezo drive at the voltage control are determined under various boundary conditions its operation in the different application. The parameters of the compound longitudinal PZT drive at the voltage control are obtained.

Keywords: Compound Piezo Drive, Model, Scheme, Voltage Control, Nanotechnology and Nanochemistry Research

INTRODUCTION

A compound piezo drive is applied for nanotechnology and nanochemistry research [1-17]. This drive based on the piezoelectric effect [18-40]. A compound piezo drive is used in scanning microscopy, adaptive optics, interferometry, nanostabilization [41-53]. The deformations of a compound piezo drive are written by using its model and scheme. The model, scheme and functions are obtained by applied the method of mathematical physics. The compound piezo drive is widely used in practice at the voltage control. Therefore, in the article considers the structural schemes of the composite piezo drive under various boundary conditions its operation.

MODEL AND SCHEMES

The model and schemes of a compound piezo drive are determined using the equation inverse piezo effect.

The equation inverse piezo effect has the form [6-52]

at the voltage control

At current the control

here 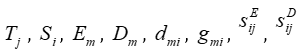 are the strength of mechanic field, the relative deformation, the strength of electric field, the electric induction, the piezo module, the piezo constant, the elastic compliances at E = const  and at D = const, i, j, m are the indexes.

In general, the equation of inverse piezo effect is written

here 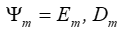 is control parameter at the control of voltage or current.

A compound drive consists from the piezo layers connected in series mechanically and parallel electrically [6 − 44]. For T-form quadripole of k piezo layer the system of equations is determined

here 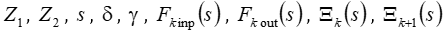 are the resistances of quadripole, the parameter, the thickness, the coefficient propagation wave, the Laplace transform of the forces at the input and output ends, the transforms of the displacements at input and output ends.

Therefore, the system of the equations for k piezo layer is obtained

This system is founded in the matrix form

At the boundary between two layers the equation of forces is determined

For a compound drive with n  layers and 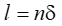 length its system has the matrix form

The equations of end forces for a compound drive are obtained

at

at

From the general equation of inverse piezo effect, the Laplace transform of force causes deformation is determined

Then the reverse coefficient for widely used in practice at the voltage control with 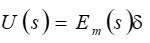  is determined in the form

This coefficient is used for the calculations of the compound piezo drive at the voltage control.

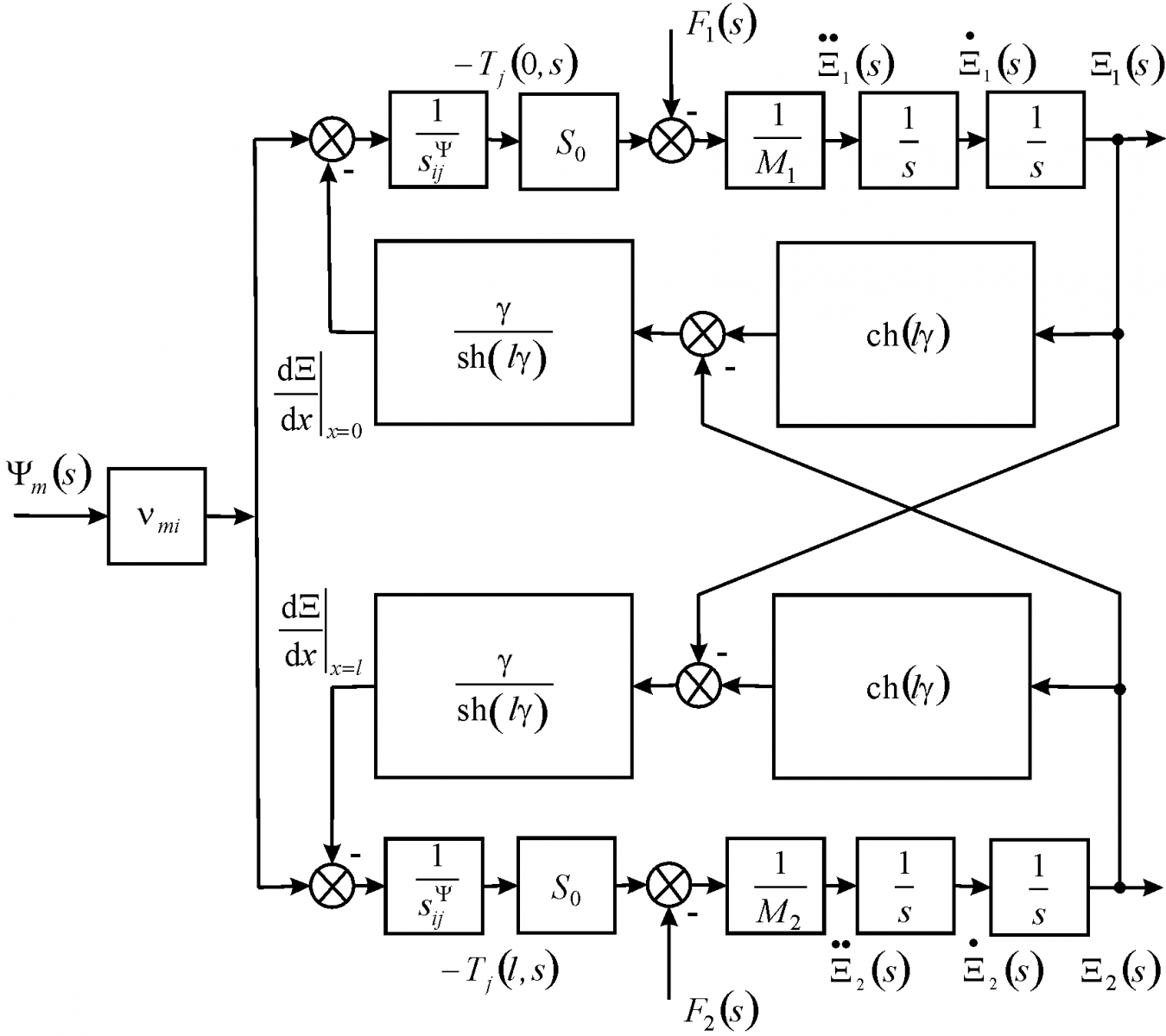
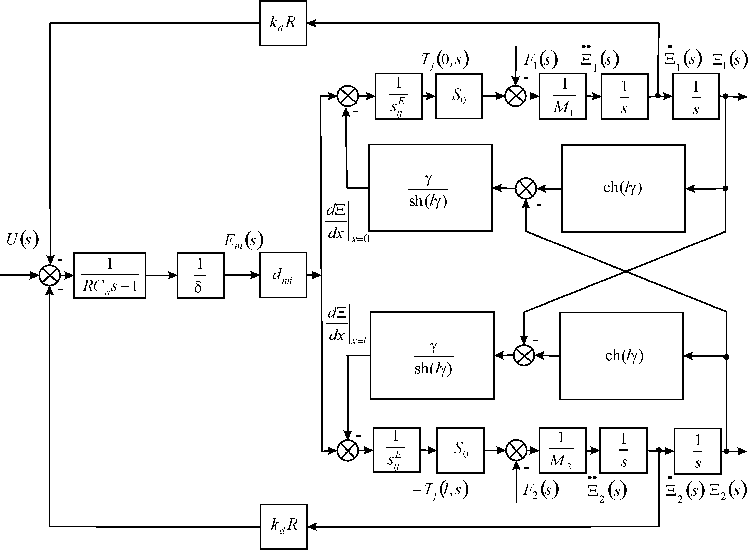
In general, the model and scheme of a compound piezo drive are founded on Figure 1

here

Figure 1. In general scheme compound piezo drive.

Its matrix equation is obtained

This functions are founded

The equation of direct piezo effect is written [6-52]

here k is the index, 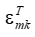is the dielectric constants. Then for the compound piezo drive at the voltage control we have its direct and reverse coefficients in the form

The Laplace transform of the negative feedback voltage on Figure 2 at the voltage control is obtained in the form

here e, R, C_n are the ends number, the resistance, the compound capacity. The sheme with negative feedbacks on Figure 2 and parameters of the compound piezo drive at the voltage control are determined.

Figure 2. Scheme compound drive at voltage control.

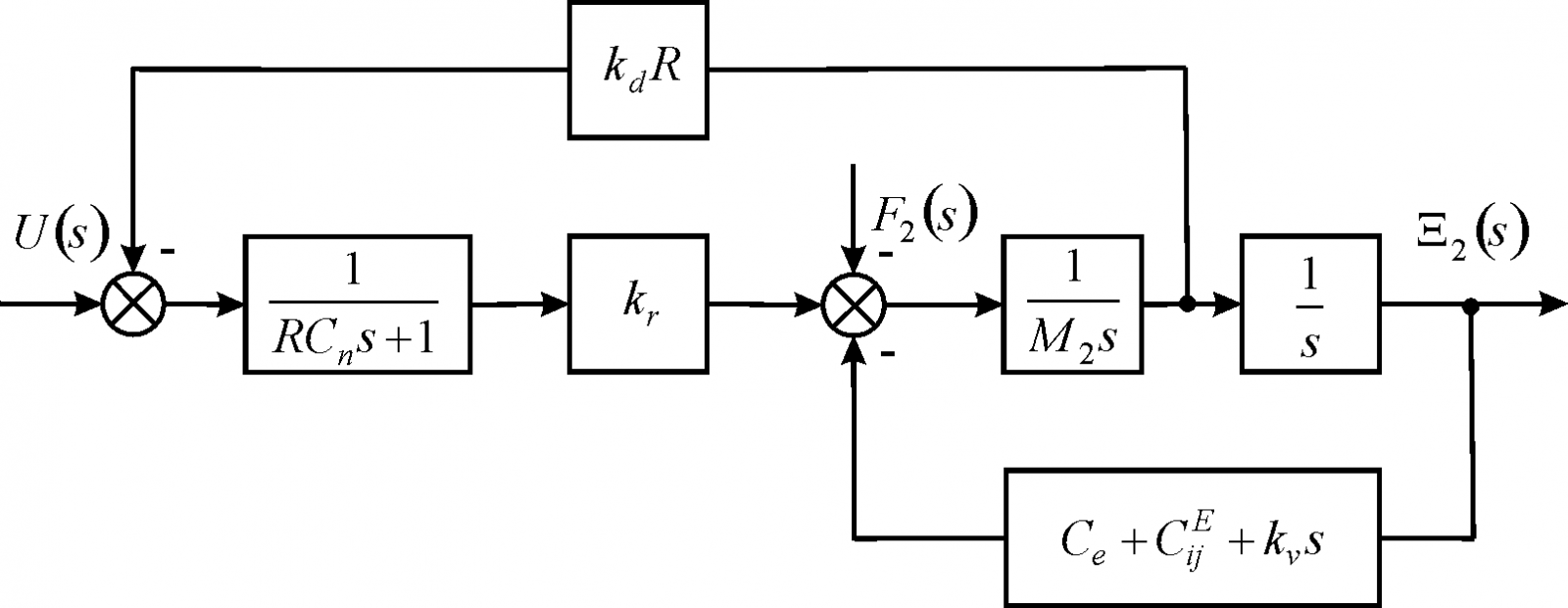
For the compound drive at the voltage control with first fixed and elastic-inertial load the scheme is obtained on Figure 3

Figure 3. Scheme compound drive at voltage control with first fixed end and elastic-inertial load.

For the compound longitudinal piezo drive at the voltage control with first fixed end and the elastic-inertial load for R = 0  its function is determined in the form

Its transient response is obtained

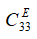
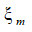
For the compound longitudinal PZT drive at the voltage control U =120 V, d₃₃  = 4∙10^-10 m/V, n = 8, M = 2 kg,  = 5.8∙10⁷ N/m, C_e = 0.6∙10⁷ N/m its parameters  = 348 nm and T_t = 1.77∙10^-4 s are obtained with error 10%.

The schemes and parameters of the compound piezo drive at the voltage control are determined.

DISCUSSION

The compound piezo drive at the voltage control is used for research in nanotechnology and nanochemistry due to its large ranges of movement and force. The model and scheme of a compound drive are founded by applied of mathematical physics method. By using the equations of quadripoles and forces its model, scheme, functions are obtained. For a compound piezo drive its system is determined in the matrix form. The scheme of the compound piezo drive at the voltage control is obtained.

CONCLUSION

A compound piezo drive for nanotechnology and nanochemistry research is applied in scanning microscopy, adaptive optics, interferometry, nanostabilization. Its model, scheme, functions are determined by applied the method of mathematical physics.

The schemes and parameters of the compound piezo drive at the voltage control are determined under various boundary conditions its operation. The parameters of the compound longitudinal PZT drive at the voltage control with first fixed end and elastic-inertial load are obtained.

REFERENCES

1. Bhushan B. (2004). Springer Handbook of Nanotechnology. New York: Springer. 1222 p.
2. Nalwa HS. (2004). Encyclopedia of Nanoscience and Nanotechnology. Los Angeles, USA: American Scientific Publishers. 10 Volumes.
3. Afonin SM. (2006). Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics. 74(3):943-948.
4. Uchino K. (1997). Piezoelectric Actuator and Ultrasonic Motors. Boston, MA: Kluwer Academic Publisher. 350 p.
5. Shevtsov SN, Soloviev AN, Parinov IA, Cherpakov AV, Chebanenko VA. (2018). Piezoelectric Actuators and Generators for Energy Harvesting. Research and Development. Springer, Switzerland, Cham. 182 p.
6. Afonin SM. (2005). Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 50(2):77-82.
7. Afonin SM. (2008). Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 53(3):137-143.
8. Afonin SM. (2006). Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics. 73(2):307-313.
9. Afonin SM. (2020). Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Appl Syst Innov. 3(4):53.
10. Afonin SM. (2021). Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Appl Syst Innov. 4(3):47.
11. Afonin SM. (2018). Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 7(1):6.
12. Afonin SM. (2019). Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 8(3):52.
13. Mason W. (1964). Physical Acoustics: Principles and Methods. Vol. 1. Part A. Methods and Devices. Academic Press, New York. 515 p.
14. Liu Y, Zhang S, Yan P, Li H. (2022). Finite element modeling and test of piezo disk with local ring electrodes for micro displacement. Micromachines. 13(6):951.
15. Jang SM, Yang SC. (2018). Highly piezoelectric BaTiO₃ nanorod bundle arrays using epitaxially grown TiO₂ nanomaterials. Nanotechnology. 29(23):235602.
16. Afonin SM. (2015). Structural-parametric model and transfer functions of electroelastic actuator for nano-and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York. pp. 225-242.
17. Afonin SM. (2017). Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 5(1):9-15.
18. Afonin SM. (2019). Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 7(2):50-57.
19. Afonin SM. (2021). Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russian Engineering Research. 41(4):285-288.
20. Afonin SM. (2024). Structural scheme of an electromagnetoelastic actuator for nanotechnology research. Chapter 45 in Physics and Mechanics of New Materials and Their Applications. PHENMA 2023. Springer Proceedings in Materials. Vol. 41. Editors Parinov IA, Chang SH, Putri EP. Springer, Cham. pp. 486-501.
21. Afonin SM. (2020). Deformation of electromagnetoelastic actuator for nano robotics system. Int Rob Auto J. 6(2):84-86.
22. Afonin SM. (2018). Electromagnetoelastic actuator for large telescopes. Aeron Aero Open Access J. 2(5):270-272.
23. Afonin SM. (2022). Piezoactuator of nanodisplacement for astrophysics. Aeron Aero Open Access J. 6(4):155-158.
24. Afonin SM (2023) Condition absolute stability of system with nano piezoactuator for astrophysics research. Aeron Aero Open Access J. 7(3):99-102.
25. Afonin SM. (2022). Piezoengine for nanomedicine and applied bionics. MOJ App Bio Biomech. 6(1):30-33.
26. Afonin SM. (2024). System with nano piezoengine under randomly influences for biomechanics. MOJ App Bio Biomech. 8(1):1-3.
27. Afonin SM. (2024). DAC electro elastic engine for nanomedicine. MOJ App Bio Biomech. 8(1):38-40.
28. Afonin SM. (2021). Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Volume 25. Eds. Bartul Z, Trenor J, Nova Science, New York. pp. 251-266.
29. Afonin SM. (2023). Structural model of nano piezoengine for applied biomechanics and biosciencess. MOJ App Bio Biomech. 7(1):21-25.
30. Afonin SM. (2020). Multilayer piezo engine for nanomedicine research. MOJ App Bio Biomech. 4(2):30-31.
31. Afonin SM. (2020). Characteristics electroelastic engine for nanobiomechanics. MOJ App Bio Biomech. 4(3):51-53.
32. Afonin SM. (2019). Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 3(2):56-57.
33. Afonin SM. (2024). Structural scheme of piezoactuator for astrophysics. Phys Astron Int J. 8(1):32-36.
34. Afonin SM. (2023). Nanopiezoactuator for astrophysics equipment. Phys Astron Int J. 7(2):153-155.
35. Afonin SM. (2023). Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. Volume 6. Ed. Min HS, B P International, India, UK. London. pp. 15-27.
36. Afonin SM. (2020). Structural scheme of electroelastic actuator for nanomechatronics, Chapter 40 in Advanced Materials. Proceedings of the International Conference on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2019. Editors: Ivan A. Parinov, Shun-Hsyung Chang, Banh Tien Long. Springer Nature, Switzerland, Cham. pp. 487-502.
37. Afonin SM. (2021). Absolute stability of control system for deformation of electromagnetoelastic actuator under random impacts in nanoresearch. Chapter 43 in Physics and Mechanics of New Materials and Their Applications. PHENMA 2020. Springer Proceedings in Materials. Volume 10. Eds. Parinov I.A., Chang S.H., Kim Y.H., Noda N.A. Springer, Switzerland, Cham. pp. 519-531.
38. Afonin SM. (2023). Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. Proceedings of the International Conference PHENMA 2021-2022, Springer Proceedings in Materials series. Vol. 20. Eds. Parinov IA, Chang SH, Soloviev AN. Springer, Cham. pp. 419-428.
39. Afonin SM. (2023). Structural parametric model and diagram of electromagnetoelastic actuator for nanodisplacement in chemistry and biochemistry research. Chapter 7 in Current Topics on Chemistry and Biochemistry. Vol. 9. Ed. Baena O.J.R., B P International, India, UK. pp. 77-95.
40. Afonin SM. (2017). Structural-parametric models of electromagnetoelastic actuators of nano- and microdisplacement for robotics and mechatronics systems. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia. pp. 769-773.
41. Afonin SM. (2018). Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia. pp. 1698-1701.
42. Afonin SM. (2020). Digital analog electro elastic converter actuator for nanoresearch. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia. pp. 2332-2335.
43. Afonin SM. (2024). Frequency method for determination self-oscillations in control systems with a piezo actuator for astrophysical research. Aeron Aero Open Access J. 8(2):115-117.
44. Afonin SM. (2024). Parallel and coded control of multi layered longitudinal piezo engine for nano biomedical research. MOJ App Bio Biomech. 8(1):62-65.
45. Afonin SM. (2024). Structural model of a nano piezoelectric actuator for nanotechnology. Russ Eng Res. 44(1):14-19.
46. Afonin SM. (2018). Electroelastic actuators for nano- and microdisplacement. SCIREA Journal of Physics. 3(2):81-91.
47. Afonin SM. (2016). Structural-parametric models of electromagnetoelastic actuators for nano- and micromanipulators of mechatronic systems. SCIREA Journal of Mechanics. 1(2): 64-80.
48. Afonin SM. (2018). Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. J Pharm Pharmaceutics. 5(1):8-12.
49. Afonin SM. (2018). Electroelastic actuator nano- and microdisplacement for precision mechanics. American Journal of Mechanics and Applications. 6(1):17-22.
50. Afonin SM. (2016). Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2(2):52-59.
51. Afonin SM. (2016). Decision wave equation and block diagram of electro magneto elastic actuator nano - and micro displacement for communications systems. International Journal of Information and Communication Sciences. 1(2):22-29.
52. Afonin SM. (2022). A piezo drive for nano chemistry research. Catalysis Research. 2(1):03.
53. Zhao C. (2011). Ultrasonic Motors Technologies and Applications. Springer: Berlin, Germany. 494 p. DOI:10.1007/978-3-642-15305-1.